crazyskwrls wrote:M = -(x+y+.5)/ (x-2y)
Easy shit
Even I know how to do that shit...
crazyskwrls wrote:M = -(x+y+.5)/ (x-2y)
Easy shit

woutR wrote:Squirt, you're a genius when it comes to raping women.
Barotix wrote:

Sacchin wrote:The dickatry is spreading around on srf faster then the flu.


woutR wrote:Squirt, you're a genius when it comes to raping women.
Barotix wrote:I did it first. 4 is a perfect square.

woutR wrote:Squirt, you're a genius when it comes to raping women.
Squirt wrote:Barotix wrote:I did it first. 4 is a perfect square.
Q: U have 4 matches put like this. Move one and only one match to make a square
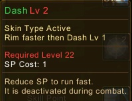

woutR wrote:Squirt, you're a genius when it comes to raping women.
What? I made a sqaure as well.Barotix wrote:I did it first. 4 is a perfect square.
Ziegfried wrote:What you do or say in any game is a small extension of who you really are. It's the anonymity that can allow them to show their true self, or who they would be if there was no "penalty" for their actions.
Da_Realest wrote:What? I made a sqaure as well.Barotix wrote:I did it first. 4 is a perfect square.



Yea, but I think your answer is the intended answer since the hint seemed to allude to the other meaning of square, a number. I didn't take the hint into account when I was thinking.Barotix wrote:Da_Realest wrote:What? I made a sqaure as well.Barotix wrote:I did it first. 4 is a perfect square.
Interesting, you used an optical illusion... before my four.
Ziegfried wrote:What you do or say in any game is a small extension of who you really are. It's the anonymity that can allow them to show their true self, or who they would be if there was no "penalty" for their actions.
crazyskwrls wrote:
well that seems impossible if u dont mind im gonna post a fun oneSpoiler!
crazyskwrls wrote:heres how u can do ten
10 = .33(repeating sign) *3
Q1: Use 6 matches to make exactly 4 equilateral triangles. Each triangle's sides has the length of the match.
Q2: Use 6 matches to make 8 equilateral triangles (any size)
(answer with a pic)
A sage undertaking to climb a mountain. To do so, he left the morning at 9am and arrives at the top at 12am. He stays overnight in the refuge and again the following day at 9am. Using the same route in reverse. He is down at 11am.
Q: Is there a place on the road where he cross at the same time two days? How to prove the existence or inexistence of such place?
NuclearSilo wrote:crazyskwrls wrote:heres how u can do ten
10 = .33(repeating sign) *3
.33 * 3 = 0.999 not 10
3.3 * 3 = 9.9 but u said no aproximation..
quiz fail :|


For equation: a^2 + b^2 = c^2
Solutions include: (3, 4, 5) OR (5, 12, 13) OR (7, 24, 25) ... infinity
(3,5,6) works because:
3^2 + 4^2 = 5^2
9 + 16 = 25 == TRUE
Now list a solution for where only integers >0 can be use (1,2,3..) for this equation:
a^3 + b^3 = c^3
First person to list any correct solution wins
Change the roman numerical 9 into a 6 with one stroke:





NuclearSilo wrote:crazyskwrls wrote:heres how u can do ten
10 = .33(repeating sign) *3
.33 * 3 = 0.999 not 10
3.3 * 3 = 9.9 but u said no aproximation..
quiz fail :|

Barotix wrote:Answer to silo: No, he never crosses it because he arrived at the final destination earlier. If we're assuming constant V then he never crosses the same path twice at the same time.